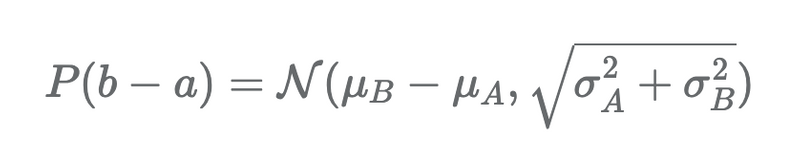A/B Test Significance in Python
A/B 테스트를 이용해 얻은 지표를 python을 통해서 통계적 유의성을 확보하기 위한 과정
아래와 같은 상황이 주어졌다고 가정해보자
사용자가 1000명 있을때 A로 550명, B로 450명이 노출되었을때
A사이트에서 48명이 전환, B사이트에서 56명이 전환
Is this a statistically significant result?통계적으로 정말 유의미하다고 말할수 있을까?
num_a, num_b = 550, 450
click_a, click_b = 48, 56
rate_a, rate_b = click_a / num_a, click_b / num_bModeling click through
버튼을 클릭할지 안할지 두개의 discrete options이 가능하다. (=binomial distribution) A사이트와 B사이트에 unknown rate 실제 클릭률은 알 수 없지만 작은 샘플을 사용하여 추정이 가능하다.
import matplotlib.pyplot as plt
from scipy.stats import binom
import numpy as np
# Determine the probability of having x number of click throughs
clicks = np.arange(20, 80)
prob_a = binom(num_a, rate_a).pmf(clicks)
prob_b = binom(num_b, rate_b).pmf(clicks)
# Make the bar plots.
plt.bar(clicks, prob_a, label="A", alpha=0.7)
plt.bar(clicks, prob_b, label="B", alpha=0.7)
plt.legend()
plt.xlabel("Num converted"); plt.ylabel("Probability");여기서 b는 edge를 갖고 있지만 A와 B에 대한 히스토그램에 따라 두 개의 임의의 점으 선택하면 A가 실제로 B보다 높을 수 있습니다.
Let’s get normal
- 클릭은 binomial distributions으로, “How long were you one the site”의 경우 Poisson distribution case
- Central Limit Theorem. 으로 invoke 할 수 있음.
- 평균 전환 또는 사이트에서 소요 된 평균 시간에 관심이 있기 때문에 기본 분포를 평균화하면 최종 추정치가 정규 분포에 의해 대략적으로 추정됩니다.
- using the normal approximation
from scipy.stats import norm
# Where does this come from? See the link above.
std_a = np.sqrt(rate_a * (1 - rate_a) / num_a)
std_b = np.sqrt(rate_b * (1 - rate_b) / num_b)
click_rate = np.linspace(0, 0.2, 200)
prob_a = norm(rate_a, std_a).pdf(click_rate)
prob_b = norm(rate_b, std_b).pdf(click_rate)
# Make the bar plots.
plt.plot(click_rate, prob_a, label="A")
plt.plot(click_rate, prob_b, label="B")
plt.legend(frameon=False)
plt.xlabel("Conversion rate"); plt.ylabel("Probability");이 방법이 첫번째보다 더좋은 방법, 방문자 수가 약간 다른 사이트 A와 사이트 B의 혼란스러운 효과를 제거했기 때문에, 따라서 우리의 질문은 여전히 같다. B의 추첨이 A의 추첨보다 높을 확률이 얼마나 되는가? 이에 답하기 위해 정규분포 된 난수의 합(또는 차이)도 정상이라는 사실을 활용한다. proof는 아래 수학식을 참고
위 식은 간단하다. 평균의 차이를 취하고, 분산을 합산하면 된다. 이후에는 z-score를 계산하고, 적절한 분포를 그린다.
z_score = (rate_b - rate_a) / np.sqrt(std_a**2 + std_b**2)
p = norm(rate_b - rate_a, np.sqrt(std_a**2 + std_b**2))
x = np.linspace(-0.05, 0.15, 1000)
y = p.pdf(x)
area_under_curve = p.sf(0)
plt.plot(x, y, label="PDF")
plt.fill_between(x, 0, y, where=x>0, label="Prob(b>a)", alpha=0.3)
plt.annotate(f"Area={area_under_curve:0.3f}", (0.02, 5))
plt.legend()
plt.xlabel("Difference in conversion rate"); plt.ylabel("Prob");
print(f"zscore is {z_score:0.3f}, with p-value {norm().sf(z_score):0.3f}")이 결과를 어떻게 표현하나? null hypothesis가 참이라고 가정할 수 있다. (B가 A보다 작거나 같음). 이는 significant result (typically p < 5%), 우리는 null hypothesis를 reject하고 B > A라는 증거가 있다고 진술 여기서는 one-talied test를 명시적으로 참고 - 우리의 질문은 B > A 이다. 다른 대안은 two-tailed test, 여기서 우리는 B가 A와 다르다는 것을 구별하고 싶다. 이 경우 p-value 값은 실제로 2 x 2.9 = 5.8% (하나가 아닌 두개의 꼬리가 있기 때문에) p-value 0.05 임계값을 고수하면 귀무가설을 기각하기 전에 더 많은 표본을 원할 것이다.
그러나 개념을 설명하고 시도하기 위해 많은 plots을 만들었다. 작은 기능을 쉽게 작성하여 이 모든 것을 단순화 할 수 있다. confidence를 원하든 p-value의 값을 원하든 최종 norm.cdf를 norm.sf로 변경하면 된다.
def get_confidence_ab_test(click_a, num_a, click_b, num_b):
rate_a = click_a / num_a
rate_b = click_b / num_b
std_a = np.sqrt(rate_a * (1 - rate_a) / num_a)
std_b = np.sqrt(rate_b * (1 - rate_b) / num_b)
z_score = (rate_b - rate_a) / np.sqrt(std_a**2 + std_b**2)
return norm.cdf(z_score)
print(get_confidence_ab_test(click_a, num_a, click_b, num_b))Can we check we’ve done the right thing?
수학을 완벽하게 수행했다고 확신하지 못하면 어떻게 해야할까? check를 brute force 할 수 있는 방법이 있을까? 우리는 normal approximation을 이용해 할 수 있다.
# Draw 10000 samples of possible rates for a and b
n = 10000
rates_a = norm(rate_a, std_a).rvs(n)
rates_b = norm(rate_b, std_b).rvs(n)
b_better = (rates_b > rates_a).sum() / n
print(f"B is better than A {b_better * 100:0.1f}% of the time")이전의 언어로 표현된 것은 A > B가 시간의 2.8%에 불가하다는 것인데, 이는 가설을 기각 할 수 있도록 통계적으로 중요하다 (A<=B) 종종 이것이 분석 솔루션이 없을 때 실제로 더 복잡한 분석을 수행하는 방법입니다. 현대 컴퓨팅의 힘은 많은 문을 열어준다.
Can we do this test even faster?
우리는 정규 분포로 가져와서 평균 차이 실험을 수행했다. 그러나 scipy는 우리의 삶을 더 쉽게 만들기 위해 그 안에 많은 것들이 숨어져 있다.
여기서 우리는 클릭률 0 또는 1의 raw results를 분포로 사용하고 inbuild t-test를 사용한다고 가정한다.
- Welsch’s t-test
from scipy.stats import ttest_ind
a_dist = np.zeros(num_a)
a_dist[:click_a] = 1
b_dist = np.zeros(num_b)
b_dist[:click_b] = 1
zscore, prob = ttest_ind(a_dist, b_dist, equal_var=False)
print(f"Zscore is {zscore:0.2f}, p-value is {prob:0.3f} (two tailed), {prob/2:0.3f} (one tailed)")