A/B 테스트를 위한 이론 정리 (확률, 통계)
통계 추론
- 전형적인 통계 추론 과정
가설을 세운다 > 실험을 설계한다 > 데어터를 수집한다 > 추론 및 결론을 도출한다.-
용어 정리
- 처리 (treatment)
- 처리군 (treatment group)
- 대조군 (control group)
- 랜덤화 (randomization): 처리를 적용할 대상을 임의로 결정하는 과정
- 대상 (subject) : 처리를 적요할 개체 대상 (유의어: 피실험자)
- 검정통계량 (test statistic): 처리 효과를 측정하기 위한 지표
그룹 A와 그룹 B를 비교하는 데 사욯아는 검정통계량 (test statistic) 또는 측정 지표에 주의를 기울여야 한다. 일반적으로 사용되는 지표는 클릭/클릭(x), 구매/구매(x)와 같은 이진변수. 측정 지표가 연속형 변수(구매액, 수익 등)인지 횟수를 나타내는 변수(입원 일수, 방문한 페이지 수)인지에 따라, 결과가 다르게 표시될 수 있다.
| 검정 결과 | 가격 A | 가격 B |
|---|---|---|
| 전환 | 200 | 182 |
| 전환(x) | 23,539 | 22,406 |
기존 가격 A, 가격 B에 따라 전환, 전환되지 않음을 측정했다면, 페이지 뷰당 수익의 결과는 다르게 나올 수 있음
가격 A의 페이지 뷰당 수익: 평균 = 3.87, SD = 51.10
가격 B의 페이지 뷰당 수익: 평균 = 4.11, SD = 62.98실험 전에 지표 또는 검정통계량을 사전에 미리 정해놓아야 한다. 실험을 수행한 뒤 나중에 검정통계량을 선택한다면 연구자의 편향이라는 함정에 빠지게 된다.
가설검정
가설검정(hypothesis test), 유의성 검정(significance test)는 전통적인 통계 분석 방법
-
용어 정리
- 귀무가설(null hypothesis): 우연 때문이라는 가설
- 대립가설(alternative hypothesis): 귀무가설과의 대조
- 일원검정(one-way test): 한 방향으로만 우연히 일어날 확률을 계산하는 가설검정
- 이원검정(two-way test): 양방향으로 우인히 일어날 확률을 계산하는 가설검정
재표본추출
랜덤한 변동성을 아보자는 일반적인 목표를 가지고, 관찰된 데이터의 값에서 표본을 반복적으로 추출하는 것을 의미한다. 머신러닝 모델의 정확성을 평가하고 향상시키는 데에도 적용 (예를 들면 의사 결정 트리 모델로부터 나온 예측들로부터 배깅이라는 절차를 통해 평균 예측값을 구할 수 있다.)
재표본추출에는 두가지 주요 유형:
- 부트스트랩: 추정의 신뢰성을 평가하는데 사용
- 순열검정 (permutation test): 두 개 이상의 표본을 함께 결합하여 관측값들을 무작위(또는 전부를)로 재표본으로 추출하는 과정
- 복원/비복원 (with or without replacement): 표본을 추출할 때, 이미 한번 뽑은 데이터를 다음번 추출을 위해 다시 제자리에 돌려 놓거나/다음 추출에서 제외하는 표집 방법
통계적 유의성과 p-value
- 자신의 실험(또는 기존 데이터에 대한 연구) 결과가 우연히 일어난 것인지 아니면 우연히 일어날 수 없는 극단적인 것인지를 판단하는 방법.
- 결과가 우연히 벌어질 수 있는 변동성의 바깥에 존재한다면 우리는 이것을 통계적으로 유의하다고 말한다.
-
용어정리
- p 값 (p-value): 귀무가설을 구체화한 기회 모델이 주어졌을 때, 관측된 결과와 같이 특이하거나 극단적인 결과를 얻을 확률
- alpha: 실제 결과가 통계적으로 의미 있는 것으로 간주되기 위해, 우연에 의한 기회 결과가 능가해야 하는 ‘비정상적인’ 가능성의 임계 확률
- type 1 error: 우연에 의해 효과가 실제 효과라고 잘못 결론 내리는 것
- type 2 error: 실제 효과를 우연에 의한 효과라고 잘못 결론 내리는 것
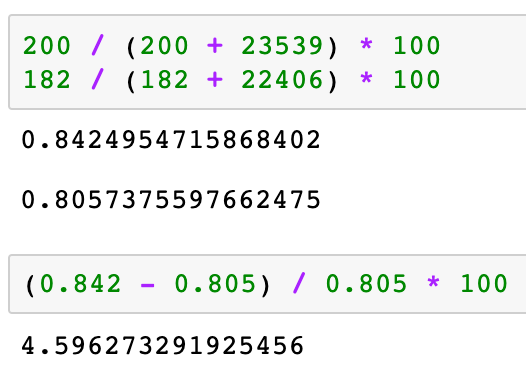
| 결과 | 가격A | 가격B |
|---|---|---|
| 전환 | 200 | 182 |
| 전환되지 않음 | 23539 | 22406 |
가격 A는 B에 비해 약 5%정도 우수한 결과를 보였다.
A는 B에 비해서 약 4.59% 정도 성능 향상이 있었다. 하지만 전환율 자체가 너무 낮아 (1% 미만), 실제 필요한 표본크기를 결정하는 데 매우 중요한 값(전환횟수)은 정작 200개 정도에 불과하다. 재표본추출 절차를 사용하면 가격 A와 B 간의 전환차이가 우연에 의한 것인지 검정할 수 있다. 여기서 우연에 의한 차이란 곧 두 전환율 사이에 차이가 없다는 귀무가설의 확률모형을 가지고 생성한 데이터의 랜덤 변이를 의미한다. 다음 순열 절차는 ‘두 가격이 동일한 전화율을 공유하는지, 이 랜덤 변이가 5%만큼의 차이를 만들어낼 수 있는지’를 묻는 질문에 대한 답을 준다.
- 모든 표본 정보가 담긴 항아리가 있다고 생각해보자. 그러면 전체 전환율은 전체 표본에서 45,945개의 0과 382개의 1이므로 0.008246 = 0.8246%라고 할 수 있다.
- 크기 23,739 (가격A)의 표본을 섞어서 뽑고 그중 1이 몇개인지 기록
- 나머지 22,588개 (가격B)에서 1의 수를 기록하자
- 1의 비율 차이를 기록
- 2~4단계를 반복
- 차이가 얼마나 자주 >= 0.0465962인가? (상승율)
Type I, Type II
- 옳은(진짜) 것임에도 올바르지 않다고 잘못 판단할 경우를 제 1종 오류 (Type I Error) 또는 알파(alpha) 오류
- 거짓인 것을 참이라고 잘못 판단하는 것을 제2종 오류(Type II Error) 또는 베타(beta) 오류라고 말함
p-value
그래프를 눈으로 보는 것보다, p값과 같이 통계적 유의성을 정확히 측정하기 위한 지표가 필요하다. 순열검정으로 얻은 결과 중에서 관찰된 차이와 같거나 더 큰 차이를 보이는 경우의 비율로 p-value를 추정할 수 있다.
유의수준(=alpha)
- 유의수준(=alpha)은 5%와 1%를 가장 많이 사용.
-
p-value의 의미: 결과가 우연에서 비롯될 확률
- 우리는 더 낮은 p값을 원하고, 결국 뭔가를 증명했다고 결론을 내릴 수 있기를 바란다. 많은 저널 편집자들이 p값을 이런식으로 해석 그러나 실제 p값이 나타내는 것은 다음과 같다.
결과가 우연에서 비롯될 확률-> 랜덤 모델이 주어졌을 때, 그 결과가 관찰된 결과보다 더 극단적일 확률
Get P-Value
def get_pvalue(con_conv, test_conv, con_size, test_size):
lift = -abs(test_conv - con_conv)
scale_one = con_conv * (1-con_conv) * (1/ con_size)
scale_two = test_conv * (1-test_conv) * (1/ test_size)
scale_val = (scale_one + scale_two) ** 0.5
p_value = 2 * stats.norm.cdf(lift, loc=0, scale = scale_val)
return p_value
# Trial 1
con_conv = 0.034351
test_conv = 0.041984
con_size = 48236
test_size = 49867
get_pvalue(con_conv, test_conv, con_size, test_size)Significance calculation method
- Bayesian
- Z Test
Confidence, Power?
확률과 통계
- 확률은 우리가 관찰한 데이터를 설명하는 방법론
- 통계는 데이터를 이용해 기저 현상을 추측
베르누이(Bernoulli) 확률변수
- 두 사건이 p와 1-p의 확률을 갖는 것
- 앞면이 나올 확률 p
- 뒷면이 나올 확률 1-p
-
확률질량함수(probability mass function)
- f(앞면) = 0.7
- f(뒷면) = 0.3
균등확률변수
- 연속확률변수는 확률변수가 연속적인 값을 가진다.
- 주사위 처럼 1,2,3,4,5,6의 정해진 값만 나오는게 아니라 주어진 범위 내에서 어떤 값이든 나옴
- 가장 간단한 연속확률변수는 균등확률변수
- 확률변수 범위가 [a,b]라면 이를 Uniform(a,b)라고 씀
- 이 확률변수는 [a,b]내에서 어떤 값이든 가능하고, 그 확률이 모두 동일
- 연속확률분포는 확률질량함수가 성립하지 않는다. (값이 연속적으로 분포)
-
확률밀도함수(probability desnity function) pdf가 있음
- 확률변수의 범위 내에서 값의 확률을 표현
- 적분하면 누적분포함수(cumulative distribution function, CDF)
- 보통 확률밀도함수는 f, 누적분포함수는 F로 표현
균등분포와 유사난수
- 베르누이 확률변수는 균등분포 Uniform(0,1)을 따르는 확률변수 u를 만들고 u < p면 앞면, u >= p면 뒷면이 되도록 구현
- ex) 주사위도 동일하게 [0,1]을 6등분
- ex) 지수확률변수는 균등분포를 따르는 확률변수 u에 -1을 곱하고 log()
비이산 불연속 확률변수
- 나무의 높이를 확률변수로 표현
- 싹 틔우기 전의 나무 높이는 값이 0인 이산확률변수 (=pie chart)
- 싹을 틔우고 나면 연속확률변수 (=histogram)
표기법, 기댓값, 표준편차
- X처럼 대문자를 이용해 확률변수
- x로 확률변수가 갖는 구체적인 값 표시
-
1차원 확률변수
- 이산: 확률질량함수
- 연속: 확률밀도함수
- 다차원확률변수: 확률질량함수와 확률밀도함수의 개념을 다차원으로 확장하여 사용
- E[X] 확률변수 X의 평균 또는 기댓값, mu_x
종속성, 주변확률, 조건부확률
- 서로 다른 확률변수 X, Y의 관계가 의미를 가지는 경우 ~
확률분포의 꼬리
-
확률분포가 평균에서 멀어져도 제법 큰 값을 나타내는 것을 흔히 확률분포의 꼬리가 두껍다고 표현
- 소득의 차이는 꼬리가 두껍고, 사람의 키는 꼬리가 얇음
-
꼬리가 긴 분포의 평균값은 추정하기도 어렵고 큰 의미를 갖지 않는다.
- 이상치를 제외하고 평균을 구하는것이 나음
-
파레토 분포는 전형적으로 꼬리가 긴 분포
- 상위 20%가 전체 양의 80%를 차지하고 있는 불균형이 심한 분포
- 표본을 추출하고 평균을 구하면 잘 수렴하지 않음
- 1000개의 샘플을 추출하면서 평균을 구한다. 표본의 크기가 늘어날수록 값이 커지는데 이는 드물게 발생한 이상치가 평균에 큰 영향을 미치기 때문이다. 이 과정을 반복하면 평균은 무한대로 발산
- 수렴하는 경우도 있지만, 수렴해도 수렴값ㅅ이 특별한 의미를 갖지 않는다. 대부분의 표본이 평균보다 훨씬 낮은 값을 갖기 때문에 좋은 대푯값이 아니다.
- 이런 경우에 대푯값을 중간값이나 사분위값을 사용하는게 좋다. (사용하기 전에 주어진 분포가 꼬리가 두꺼운 분포인지 확실히 조사)
이항분포
- 이항분포는 B(n,p) 참일 확률이 p인 베르누이 확률변수를 n번 시행했을때 나온 값의 합
- 값의 범위는 [0,n], 기댓값은 np, 확률질량함수의 최댓값도 np, 표준편차는 root(n)에 비례, n이 증가할수록 np근처가 나올 확률이 증가
푸아송(Poisson) 분포
- 시간에 따라 발생하는 독립 사건을 모사하는 확률변수 모델
- 웹사이트의 하루 방문자 수를 푸아송 분포로 나타낼 수 있다.
- 이항분포 B(n, p)에서 n이 아주 크고 p가 아주 작은 경우를 가정
- 푸아송 분포는 확률질량함수를 갖음
정규분포
- 가우스 분포라고도 부르며 확률분포 중 가장 널리 쓰임
- 종모양의 분포
- 정규분포의 확률밀도함수는 아래와 같음
- 정규 분포는 꼬리가 매우 가늘다 (=이상치가 나타날 확률이 매우 낮다.)
- 정규분포를 가정하고 커브피팅을 한다면 이상치를 제거하는 전처리 작업이 필요
-
(중요) 이항분포, 푸아송 분포를 포함해 대다수 분포에서 충분히 많은 값을 샘플링한 값의 평균은 정규분포로 수렴한다.
- 우리가 다루는 데이터는 대게 모집단이 아니라 모집단에서 샘플링한 값이기 때문에 정규분포를 따르는 경우가 많다 (=중심극한정리 central limit theorem)
다차원 정규분포
- 대부분 분포는 1차원 변수를 가정
- 정규 분포는 어떤 차원으로든 표현이 가능하다. (2차원에서는 산을 상상)
- 다차원 정규분포의 확률밀도함수
- 1차원 정규분포의 특징을 그대로 갖는다.
- 중심극한정리도 적용, 대부분 값이 평균 근처에 존재한다는 특징도 적용
지수분포
- 지수분포의 확률밀도함수
-
두 사건이 일어날 간격을 확률변수로 모델링하는 경우 사용
- 예) 가게에 손님이 들어오는 시간 간격이 해당
로그 정규분포
- 로그 정규분포는 값에 로그를 취하면 정규분포를 따르는 확률분포
- 값에 로그를 취해야 하므로 범위가 양수로 제한
- 정규분포의 확률밀도함수
- 비대칭 (피크를 기준으로 왼쪽은 급격하게 떨어지지만 오른쪽은 천천히 떨어지고 굵은 꼬리를 갖는다.) (=이상치가 존재할 확률이 높다)
엔트로피(entropy)
- 확률분포의 무작위성을 측정하는 방법
- 분산이 아주 작은 정규분포는 거의 항상 평균에 아주 까까운 값을 가지게 되므로 무작위성이 낮다.
-
이산확률변수 X를 가정
- 확률변수를 샘플링한 결과가 얼마나 놀라운지 측정하고 이 놀라운 정도의 평균을 엔트로피가 되도록
- 확률이 낮은 일이 일어날수록 더놀라움
통계
베이지안과 빈도론자의 비교
- 데이터와 모델의 관계를 정의하는 방법이 차이
-
전통적인 방식은 빈도론자의 접근 방식
- 어떤 분포를 사용하는지는 사용자의 선택이지만 이후엔 데이터를 이용해 모델의 최적 매개변수를 구한다. 이 과정에서는 어떤 모델이 주어진 데이터를 잘 설명하고 주어진 결과를 출력할 만한지가 중요하다. 이렇게 구한 최적 매개변수를 적용한 모델로 새로운 결과를 예측
- 베이지안 통계학은 조금 더 복잡한 과정을 거친다. 최적 매개변수를 구하는 것이 아니라 매개변수의 신뢰도를 같이 구한다. 이 신뢰도는 매개변수에 대한 확률분포로 표현되며 특정 데이터셋에 국한된 것이 아닌 현실 세계의 데이터 전체에 대한 특징 (=이를 사전 prior 분포). 우리가 사용할 데이터가 주어지기 전부터 존재하는 정보. prior를 이용해 사전 분포를 조금씩 수정. 즉 주어진 데이터와 사전분포를 이용해 최적의 매개변수를 구한다. 새로운 결과를 예측하려면 모델을 하나만 이용하는 것이 아니라 신뢰도를 고려하여 여러 모델의 결과의 평균을 구하고 이를 이용
- 좋은 사전 분포를 구할 수 있거나 주어진 데이터가 편향되어 있다면 베이지안이 잘 작동, 반면 전통적인 방식은 사용이 편리
가설검정
- 데이터를 이용해 어떤 가설이 참인지 거짓인지 예측
- 통계적 지식으로 이해하는 과정
-
동전을 던졌을때 앞면이 9번, 뒷면이 1번 나왔다면 이 동전은 공정한 동전일까?
- 이 데이터만 가지고 가설을 판단하는 것은 불가능
- 정확한 추정을 하려면 prior probability (선험적 확률), 즉 일반적으로 동전이 평향되어 있을 확률을 알아야 한다.
- (x) “이 동전이 편향된 동전일 확률”
- (o) “이 동전이 편향된 동전이라면 주어진 데이터가 나올 확률이 얼마나 되나?” (=10번 중에 9번 앞면이 나오는게 말이돼?)
-
공정한 동전이라고 가정하고 확률을 구해보자
- 동전은 앞뒤가 있으므로 10번 던지면 모든 경우의 수는 2^10 = 1024고, 발생활 확률은 동일하다.
- 10번중에 9번 앞면이 나오는 편향된 결과는 몇 종류가 있을까?
- 10번 모두 앞면이 나오는 경우 1
- 앞면이 9번 나오는 경우의 수는 10번 중 1번만 뒤면이 나오는 수와 같으므로 10가지
- 10번 모두 뒷면이 나오는 경우는 1
- 뒷면이 9번 나오는 경우 10
- 총 22가지, 22 / 1024 = 0.0214이므로 공정한 동전인데 주어진 데이터 만큼 결과가 편향될 확률은 2%뿐이다.
- 동전이 편향되었는지가 궁금, 이를 밝히기 위해 동전이 공정하다는 가설을 세웠다. 이렇게 통계분석을 위해 세우는 가설 중 패턴이나 사건이 존재하지 않는다고 가정하는 가설을 귀무가설(nulll hypothesis)라고 한다. 우리의 목표는 귀무가설이 거짓!
- 검정통계량 (test statistic)은 데이터에 나타난 패턴을 요약하는 값.
-
귀무가설에 기반한 검정통계량의 분포를 계산하면 귀무가설을 검정할 수 있다.
- 예) ‘앞면’의 횟수가 검정통계량
- 문제가 복잡해질수록 검정통계량을 효과적으로 설정하는게 중요
-
p-value
- 데이터에 나타난 검정통계량이 얼마나 낮은 확률을 가지는지 조사
- 검정가설은 패턴이 존재하지 않을 것을 가정한 가설, 검정가설에 의한 검정통계량이 낮은 확률을 가질수록 검정가설은 설득력을 잃는다. 보통 p-value값이 0.05보다 낮으면 통계적으로 유의미한 결과라고 간주
- 0.07이 나오면? 세운 가설이 무의미? No, 주어진 데이터의 개수와 패턴의 선험적 확률, p-value에 따라 상황을 정확하게 이해하는게 중요
다중 가설검정
- 통계분석을 하다 보면 가설을 여러 개 세우게 된다.
-
가설 여러개 세울때 생기는 문제 (p-value를 더욱 엄격하게 적용해야 전체 실험이 유의미해짐) 본페로니(Bonferroni) 수정법이 있음.
- 본페로니는 모든 가설이 서로 독립이라고 가정 (현실은 그렇지 않음))
- 필요 이상으로 낮은 p-value의 값을 요구하게 된다. (거의 사용 x)
매개변수 추정
- 가설검정은 구체적인 값을 알아내지 못한다. 따라서 주어진 데이터를 모델링하고 매개변수를 추정하려면 다른 방법을 사용해야 한다.
-
매개변수 추정하기 위해서 주어진 데이터의 분포를 보고 적당한 확률 모델을 가정
- 데이터 분포가 정규분포? 평균(mu)와 표준편차(sigma)를 추정하는 문제
-
표본평균과 표본편차는 모두 검정통계량에 해당. (새로운 데이터를 수집하면 이 값은 조금씩 달라짐) 따라서 추정한 표본평균과 표본표준편차가 실제값, 즉 모집단의 평균, 표준편차와 비슷한 값을 가지는지 따져야 한다.
- 데이터를 기반으로 값을 추정할 때는 추정값과의 일관성(consistency)과 불편향성(unbiasness)으로 추정값을 평가
- 일관성: 표본의 크기가 증가할수록 추정값이 실제값에 가까워지는 것
- 불편향성: 추정값의 기댓값이 실젯값과 같은 것
t 검정
- 두 분포의 모평균이 다른지 검정하는 과정
- 가설 검정 중 가장 복잡한 방법
- 관측값이 연속적으로 분포할때 사용한다
-
예) 콜레스테롤 수치를 낮춰주는 약을 복용한 환자와 복용하지 않은 환자를 대상으로 콜레스테롤 수치를 측정한 데이터를 어떻게 분석하면 약의 효능을 인정할 수 있을까?
- 두 환자군의 콜레스테롤 수치를 히스토그램으로 그려보면 된다.
- 히스토그램이 겹치지 않는다면 차이가 존재
- 히스토그램이 겹친다면 두가지 값(평균, 분산)을 봐야 한다.
- 어떤 경우든 데이터가 충분히 많다면 직관적인 결론을 내릴 수 있다.
- p-value로 직관을 정량화하는 것은 훨씬 복잡하다.
from scipy.stats import ttest_ind
# 분산이 같다는 가정하에 t-test
t_score, p_value = ttest_ind([1,2,3,4], [2,2,2,3,5])
# 분산이 다른 경우
t_score, p_value = ttest_ind([1,2,3,4], [2,2,2,3,5], equal_var=False)- 귀무가설을 세우고 검정통계량을 고른다. 그리고 검정통계량의 값에 따라 귀무가설을 기각할 확률을 구한다.
-
t 검정에는 두 가지 귀무가설이 존재
- 두 데이터는 같은 분포의 표본
- 두 데이터는 평균은 같지만 분산이 다른 두 분포의 표본
- t 검정은 가설을 검증할 뿐 실제 모델의 매개변수는 추정하지 않는다.
-
t 검정의 검정통계량은 다음 가설에 따라 이루어진다.
- 두 집단의 분포는 정규분포를 따른다.
- A와 B집단 평균 mua, mub를 추정하고 두 값의 차이를 본다.
- 데이터가 충분하다면 mua와 mub가 실제 평균과 유사하게 나온다. 귀무가설이 참이라면 두 값의 차이가 작다.
- 두 분포의 분산이 크다면 상대적으로 mua와 mub도 큰 차이를 가져야 귀무가설이 거짓
- T값의 분포는 t-분포(평균이 0이고, 표준편차가 1인 정규분포와 비슷하지만 두꺼운 꼬리를 갖는다.)를 갖는다. 계산한 T 값이 꼬리에 속할수록, 즉 아주 작거나 아주 클수록 두 집단이 서로 다르다는 가설이 힘을 얻는다.
-
데이터가 정규분포를 따르는지 검정하는 방법은 z 검정을 많이 사용
- z검정은 주어진 데이터가 정규분포를 따른다는 귀무가설을 세우고 데이터의 특징값을 계산하여 이를 검정.
# z검정
from scipy.stats import normaltest
z_score, p_value = normaltest(my_array)신뢰구간
- 매개변수를 추정할 때 추정값의 신뢰도를 알면 유용한 경우가 많다.
- 추정치가 4.1+-0.2로 표현하면 여기서 0.2가 클수록 신뢰도가 낮아짐
- 표본평균의 신뢰구간 (표본 평균이 아닌 다른 값의 신뢰구간을 구할 때는 해당 수치를 평균을 구하는 형태로 바꿔야 한다.)
- 신뢰도는 보통 평균의 ‘표준오차’를 이용한다. (4.1이 표본평균, 0.2가 표준오차)
from scipy.stat import sem
# 표준 오차 계산
std_err = sem(my_array)- 중심극한정리(Central limit theorem)에 따라 반복적으로 표본평균을 구하면 그 값은 정규분포를 따른다. 표준 오차를 이용하면 90%, 95%, 99%등의 신뢰구간을 구할 수 있다.
- 예를 들어 95% 신뢰구간의 의미는 해당 범위에 모평균이 존재할 확률이 95%
- 표본을 추출하여 표본평균을 구하는 과정을 반복하면 매번 다른 신뢰구간이 나오는데 그중 95%는 모평균을 포함하고 있다는 의미 (=신뢰구간이 작을수록 좋음)
- 신뢰구간을 줄이려면, 즉 추정값을 정교하게 하려면 표본 수를 늘려야 한다.
베이지안 통계학
- 전통적인 통계학은 주어진 데이터로 매개변수를 추정하고 신뢰구간을 계산
-
베이지안 통계학은 매개변수 간의 의존관계를 가정
- 의존관계는 해당 분야의 지식에 근거하여 데이터와 별도로 분석 과정에서 사람이 설정
- 베이지안 통계학은 사전 지식을 이용해 분석하기 전부터 매개변수의 분포를 가정하고 데이터가 추가되면 이를 갱신
-
베이지안 통계학의 근간은 베이지 정리
- 확률변수 T, D가 있을때 조건부 확률 P(T|D)
- P(T|D) = P(T)P(D|T) / P(D)
- T를 실젯값, D를 주어진 데이터로 가정
- P(T): 선험적 확률, 사전 지식을 이용해 얻은 T의 분포
- P(D|T): 우도(likelihood), 특정 매개변수 T를 가정할 때 주어진 데이터가 발생할 확률
- P(D): 가능한 모든 매개변수를 가정할 때 주어진 데이터가 발생할 확률
- 예) 머리카락 길이로 사용자의 성별을 추정 (전체 사용자의 성비가 2:1로 남성이 더 많다고 가정) 이 가정은 선험적 확률을 제공
P(여성|장발) = P(여성)P(장발|여성) / P(장발)
P(장발) = 1/3P(장발|여성) + 2/3P(장발/남성)
P(여성) = 1/3나이브 베이즈
- 베이즈 정리에서 P(D|T)를 구하는게 골치 아플때가 있다.
-
예) 당뇨병 환자의 혈중 글루코오스 농도와 혈당량이 주어진 데이터라면 D는 2차원 벡터로 구성
- 혈중 글루코오승 농도와 혈당량은 서로 영향을 주고받는 확률변수인데, 이 관계를 정확하게 파악하기란 매우 어렵다.
- 위와 같은 현실적인 문제 때문에 나이브 베이즈(naive Bayes)를 사용한다. 나이브 베이즈는 데이터의 각 차원이 서로 독립이라고 가정하고 사용
베이지안 네트워크
- 특징값의 상호작용을 감안하는 것은 데이터가 많이 필요하다는 단점이 있고, 나이브 베이즈는 이를 너무 단순하게 한다는 문제가 있음 그 중간에 위치한 방법이 바로 베이지안 네트워크 (Bayesian networks)
-
베이지안 네트워크는 사전 지식을 이용해 변수 간 상관관계를 정의한다.
- 인과관계를 나타낸다. (예: 성별 -> 머리카락 길이 -> 머리감는시간)
- 인과관계는 조건부확률로 나타낼 수 있고 관찰한 값에 따라 변수 간 독립 여부가 복잡하게 결정
-
변수의 관계를 직접 정의하고 나면 이에 해당하는 조건부확률만 모델링하면 됨
- (x) P(성별, 머리카락길이, 머리 감는시간, 머리끈 사용여부) 전체 모델링
- (o) P(머리카락 길이|성별), P(머리 가믄시간|머리카락길이), P(머리끈 사용 여부 |머리카락길이)를 모델링
- 보통 해당 분야의 지식에 기반해 변수의 관계를 직접 정의하고, 데이터를 이용해 확률밀도함수의 매개변수를 추정하고 결과를 평가
선험적 확률 추정
-
베이지안 분류기를 사용하려면 선험적 확률을 알아야 한다. (그러나 상황에 따라 알려지지 않은 경우가 있음)
- 단순한 방법으로 선험적 확률을 추정해 적용 (예를 들어 성별은 남녀가 50%)
-
고차원적으로 설명하면 엔트로피를 극대화하는 선험적 확률을 이용하는 것
- 확률분포의 엔트로피는 분포의 무작위성을 나타내기 때문에 엔트로피를 극대화 하는 것은 선험적 확률을 모르는 것과 같은 가정을 의미
- 엔트로피를 극대화 한다는 얘기는 무작위성이 커지고 놀라움을 많이주는… 부정확한, 크다는것은 선험적 확률을 모르는것
유의성검정과 T-검정
- 우리가 받는 데이터가 모집단 데이터가 아닌 표본 데이터
-
예) 대통령선거, 후보의 지지율에 대해서 궁금해요!
- A, B 후보의 지지율
- 모집단: 투표권자
- 전체를 할 수 없으니, 3000명을 대상으로 조사
- A 후보 지지율이 0.45
- B 후보 지지율이 0.47
- 표본으로 모집단 전체를 판단, 해석을 할 수 있을까?
- 해석할때는 확률적 분석을 통해서 해석
- 유의확률로 계산이 필요하고 유의성검정이 꼭 필요하다
- 유의확률: p-value
-
유의수준: 유의 수준의 기준 (0.05, 0.01, 0.001)
- 숫자가 작을 수록 엄격
-
유의확률 > 유의수준 => 비유의적
- 귀무가설이 기각
- 유의확률 < 유의수준 => 유의적
t-검증 (t-test)
독립 표본 T 검정 (Independent two sample T test)
가장 먼저 접근 할 수 있는 통계분석 방법은 두 집단 각각을 대표할 수 있는 값을 도출한 후 이 값이 집단간에 서로 차이가 있느냐에 대한 분석이다. 대표값이 평균이라고 하면 일반적으로 쉽게 접근할 수 있는 방법이 바로 indpendent two sample T test 이다.
-
모수적 검정 방법(parametric test)
- Student’s T test
- 두 집단 각각에서 추정된 분산(variance)이 동일 할때 사용
- Welch’s T test
- 두 집단 각각에서 추정된 분산(variance)이 다를때 사용
- 두 집단의 분산이 동일한지 여부는
Levene's test방법을 이용해 분석 가능
-
적용하기 위한 3가지 조건
- identical interval and continuity
- independence
- nomality
indentical interval and continuity
-
동일 간격을 가지는 연속형 수치에만 t-test 검저 사용 가능
- 키 10cm, 20cm 두배 크다 가능 (ratio scale)
- IQ 100, 200 두배 똑똑? 불가능 (interval scale)
- 반 1등, 2등의 경우 3위 4위가 동일한 차이라고 말할수 없음 연속형이 아니지만 순위 정보를 가진 자료를 서열척도 혹은 순위척도(ordinal scale) 자료라고 한다. 이러한 순위 척도 자료는 독립 표본 T 검정을 사용할 수 없고, 비모수적 검정(non-parametric test)인 맨-휘트니스 U검정(Mann-Whitney U test)를 이용해 두 집단의 차이를 분석
independence
- 두 집단을 구성하는 구성원이나 구성물이 독립
-
두 집단이 독립이 아닐때는 대응표본 T 검정 방법(paired samples T test)를 사용해야 한다.
- 예) A라는 사람에게 약을 주고 전후를 비교할때
normality
- 우리가 수집한 데이터가 특정 값에 편중됨 없이 적절히 잘 수집되었나를 확인하는 과정 (=정규 분포))
- “각 집단에서 30개 이상의 측정값을 확보한 경우에는 자료의 분포는 정규성을 가진다.” 여기서 중요한 사실은 위 언급한 자료의 정규성이
각 집단에서 확보한 30개 측정값자체의 정규성을 의미하는 것이 아니라 30개 측정값의 평균이 가지는 정규성 이라는 것 - 즉, 독립 표본 T 검정에서는 두 집다에서 측정한 수치 하나 하나를 비교하는 것이 아니고 각 집단의 평균을 비교하는 것이기 때문에 자료의 정규성 이라는 것 또한 각 평균이 가지는 정규성을 의미
- 샘플의 표본수가 30개 이상일 경우 표본 평균, 모집단의 자료 분포와는 상관없이 정규분포를 따른다 (보다 정확히는 정규 분포에 가까워 진다) 라는 것은 중심극한정리(central limit theorem)를 통해 증명된 사실
- 샘플이 30개 미만이 표본집단 자체가 정규성을 만족하지 못할 경우에 순위 척도 자료인 경우에 사용하는 비모수적 검정방법인 mann-whitney U test를 사용할 수 있다.
- 자료의 정규성 검증 방법은
Kolmogorov-Smirnov test와Shapiro-Wilk test방법이 있다.
파이썬으로 구현하기
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html
- Independent two-sample t-test
- 서로 다른 두 집단의 차이를 분석
- 두개의 표본의 크기와 분산이 같을때 사용하는 것
N_1 = 10
mu_1 = 0
sigma_1 = 1
N_2 = 10
mu_2 = 0.5
sigma_2 = 1
np.random.seed(0)
x1 = sp.stats.norm(mu_1, sigma_1).rvs(N_1)
x2 = sp.stats.norm(mu_2, sigma_2).rvs(N_2)
ax = sns.distplot(x1, kde=False, fit=sp.stats.norm, label="1번 데이터 집합")
ax = sns.distplot(x2, kde=False, fit=sp.stats.norm, label="2번 데이터 집합")
ax.lines[0].set_linestyle(":")
plt.legend()
plt.show()참고
ANOVA VS t-test
- ANOVA(Analysis of Variance, 분산분석)는 그룹 3개 이상을 비교해서 특정 그룹이 다른 그룹들과 통계적으로 차이가 있는지를 확인
- t-test는 control, experimental group 두개를 비교 (두개 그룹의 통계적인 차이가 있는지 확인)
- 두개 모두 variance를 비교하는 테스트 (기본 가정은 샘플 집단이 정규분포를 가진다는 가정 (종모양)
t-test에서의 one-tailed or two-tailed hypothesis
one-tailed test
- 두 변인 중에서 어느 한 변인의 가능성이 크다고 여길때
- 어느 한 쪽으로 가능성이 더 열려 있음
-
예시
- 영어과 학생의 영어성적이 더 좋을 것이다. (one-tailed)
- 이 약을 타면 세포가 더 죽는다
two-tailed test
- 두 변인이 차이는 있지만 그 가능성을 예측하기 어려울때
- 어느 쪽이 더 큰지 짐작하기 어려워 two-tailed
- 양방향으로 이동시킬수 있다고 예측될 경우에 사용
-
예시
- 여학생과 남학생 사이에 영어 성적의 차이가 있을 것이다. (two-tailed)
- 더 죽을수도 있고, 더 잘 살수도 있다.
이항 검정 (Binominal Test)
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.binom_test.html
- 이항검정은 이항분포를 이용하여 베르누이 확률변수의 모수 mu에 대한 가설을 조사하는 검정 방법
- Bernoulli 실험에서 성공 확률이 p라는 귀무 가설에 대한 two-sided test
- 두 가지 값을 가지는 확률변수의 분포를 판단하는데 도움
Python
-
parameters
- x: the number of successes
- n: the number of trials
- p(default: 0.5): hypothesized probability
- alternative(default: “two-sided”) : indicates the alternative hypothesis
- return: p-value
scipy.stats.binom_test(x, n=Nonem p=0.5, alternative='two-sided')Types of Error
- confidence level은 probability of not making Type 1 Error
- Higher this value,larger test sample needed
-
statistical power
- probability of finding a statistically significant result when the Null Hypothesis false
제 1종 오류
- 귀무가설이 옮음에도 불구하고 기각할 확률 a
참고
Power 검정력
- 대립가설이 사실일때, 이를 사실로서 결정할 확률
- 검정력이 90%라고 하면, 대립가설이 사실임에도 불구하고 귀무가설을 채택할 확률(2종 오류)의 확률은 10% 이다.
- 대립가설 하의 a=a1에서 귀무가설을 기각시킬 확률은 a=a1에서의 검정력이라고 한다.
- 검정력이 좋으면, 2종(beta error) 오류를 범할 확률은 작야짐
- confidence level이 클수록 power는 줄어든다.
- 유의한 차이를 통계적으로 유의하다고 결론 내기 위해서는 충분한 검정력을 지녀야 한다.
- 샘플사이즈가 많아질수록 power sms wmdrkgksek.
- one minus confidence level은 type one error
- confidecne level이 작을수록 type one error (alpha)는 커진다.
- type one error가 커질수록 type two error(beta)는 작아진다.
- power는 1 - beta의 값으로 계산된다. beta가 작을수록 power는 커진다.
- 일반적으로 power가 0.8 이상이 되기를 바란다.
- null hypothesis를 correctly rejects 하는 확률 (alternative hypothesis가 true 일때)
-
Two main things affect statistical power:
- sample size(more is better)
- Effect size(more is better)
Get Power
from scipy import stats
def get_power(n, p1, p2, cl):
alpha = 1 - cl
qu = stats.norm.ppf(1 - alpha/2)
diff = abs(p2-p1)
bp = (p1+p2) / 2
v1 = p1 * (1-p1)
v2 = p2 * (1-p2)
bv = bp * (1-bp)
power_part_one = stats.norm.cdf((n**0.5 * diff - qu * (2 * bv)**0.5) / (v1+v2) ** 0.5)
power_part_two = 1 - stats.norm.cdf((n**0.5 * diff + qu * (2 * bv)**0.5) / (v1+v2) ** 0.5)
power = power_part_one + power_part_two
return (power)- n: sample size
- control group mean (p1)
- testgroupmean (p2)
- confidence interval(cl)
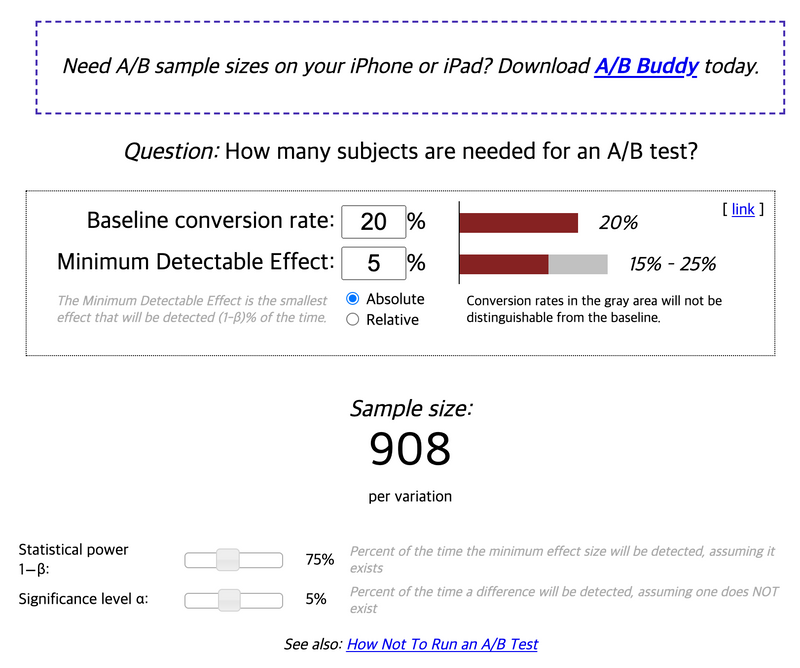
Get Sample Size
def get_sample_size(power, p1, p2, cl, max_n=100000000):
n = 1
while n <= max_n:
tmp_power = get_power(n, p1, p2, cl)
if tmp_power >= power:
return n
else:
n = n + 100
return "Increase Max N Value"
# Trial 1
conversion_rate = 0.03 # baseline conversion rate
power = 0.8 # statistical power (1-beta) = power
cl = 0.9 # confidence interval
percent_lift = 0.1
conversion_rate_p2 = conversion_rate * (1 + percent_lift)
get_sample_size(power, conversion_rate, conversion_rate_p2, cl)참고
-
power
-
sample size
- https://medium.com/@robbiegeoghegan/implementing-a-b-tests-in-python-514e9eb5b3a1
- https://www.evanmiller.org/ab-testing/sample-size.html
- https://www.qualtrics.com/experience-management/research/determine-sample-size/
- https://medium.com/@henryfeng/handy-functions-for-a-b-testing-in-python-f6fdff892a90
- https://exp-platform.com/Documents/2017-08%20ABTutorial/ABTutorial_2_statFoundations.pdf
베이즈 통계학
- 베이즈 통계학은 표본 데이터가 적더라도 추정할수 있는 발생 확률을 추정할 수 있다는 특징이 있음
-
장점
- 무언가 새로운 정보가 들어올 때마다 추측하는 확률도 변해간다(정밀도가 높아진다) = 베이즈 갱신
Confidence Level
- 얼마나 확신하는지에 대한
- 특정 x의 값이 N%의 확률로 a, b의 사이에 있을 확률을 말한다.
- 입력값으로 값들의 array
Mean Confidence Interval
import numpy as np
import scipy.stats
def mean_confidence_interval(data, confidence=0.95):
a = 1.0 * np.array(data)
n = len(a)
m, se = np.mean(a), scipy.stats.sem(a)
h = se * scipy.stats.t.ppf((1 + confidence) / 2., n-1)
return m, m-h, m+h
print(mean_confidence_interval([1,2,3,4,5,6,7]))-
sem: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.sem.html- compute standard error of the mean
-
t.ppf: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.t.html- percent point function (inverse of cdf - percentiles)
Confidence Interval
def get_ci(lift, alpha, sd):
val = abs(stats.norm.ppf((1-alpha)/2))
lwr_bnd = lift - val * sd
upr_bnd = lift + val * sd
return (lwr_bnd, upr_bnd)
test_conv = 0.102005
con_conv = 0.090965
test_size = 56350
con_size = 58583
lift_mean = test_conv - con_conv
lift_variance = (1 - test_conv) * test_conv /test_size + (1 - con_conv) * con_conv / con_size
lift_sd = lift_variance**0.5
get_ci(lift_mean, 0.95, lift_sd)
## (0.007624337671217316, 0.014455662328782672)Get Confidence A/B test
def get_confidence_ab_test(click_a, num_a, click_b, num_b):
rate_a = click_a / num_a
rate_b = click_b / num_b
std_a = np.sqrt(rate_a * (1 - rate_a) / num_a)
std_b = np.sqrt(rate_b * (1 - rate_b) / num_b)
z_score = (rate_b - rate_a) / np.sqrt(std_a**2 + std_b**2)
return norm.cdf(z_score)
print(get_confidence_ab_test(click_a, num_a, click_b, num_b))참고
- https://operatingsystems.tistory.com/entry/Data-Mining-Confidence-level
- https://datascienceschool.net/view-notebook/e6c0d4ff9f4c403c8587c7d394bc930a/
- https://stackoverflow.com/questions/15033511/compute-a-confidence-interval-from-sample-data
Udacity
- 시간이 얼마나 필요할지
- 비교하는 baseline이 무엇인지
학생들의 참여도를 높히는 (Funnel)
- Homepage visits
- Exploring the site
- create account
- complete
- sharing
- …
Experiment
-
total number of course completed (x)
- 너무 많은 시간이 걸린다.
- number of clicks (x)
- number of clicks / number of page views (=ctr) (x)
- unique visitors who clicks / unique visitors to page (=click through probability) (o)
Rate != Probability
- you use a rate when you want to measure the usability of the site
- probability when you want to measure the total impact
- you want to measure the usability of a particular button, you use a rate because the users have a variety of different plces on the page that they can actually choose to click on And so the rate will say how often do they actually find that button.
- if you just want to know how often users went to the second level page on you site, you use a probability, because you don’t want to count if users just doubl-clicked, or did they reload, or all of those types of issues.
-
어떻게 probability를 계산을 해야하나?
- 모든 페이지 뷰에 event를 캡쳐하고
- 사용자가 클릭을 하는 이벤트 캡쳐
- sum the page views / sum the clicks
- each page view of the child clicks
- one child click per page view
Review Statistics
binomial distribution, confidence level, hypothesis test
우리가 계산할 지표는 확률 (클릭할지 안할지) 결과가 우연히 발생했을 가능성이 있다.
Designing an Experiment
- Choose “Subject”
- Choose “Population”
- Size
- Duration
Analyzing Results
Single Metric Multiple Metric Gotchas
https://classroom.udacity.com/courses/ud257/lessons/4085798776/concepts/41147386150923
RPM의 경우 클릭률과 클릭당 비용으로 함께 표시된다. RPM으로 한방향 이해하기 위해 클릭당 비용의 클릭률을 볼 수 있기를 바란다. multiple metric은
전체를 단일하고 싶어하는 이유로
OEC는
머무르는 시간과 클릭이 서로 다른 방향으로 움직이고 있다. 이 균형 잡기 장기에 도움이 될 수 있는 것은 사이트 재 방문과 같은 투자 클릭 수 증가와 같은 단기적인 일일 측정 항목이 있습니다.
OEC는 하나가 아니라 두개의 균형! 비즈니스 분석으로 시작 25%의 수익에 75%의 사이트 사용 증가를
어떤 실험을 했는지 말은 안하고, 수치만 보여주고 결정만했음 이를 사용해서 실제로 OEC의 가중치를 다시 도출 실제로는 결정을 내리기 위해 OEC를 사용하지 않는다. OEC가 있는 것은 공식적인 숫자 일 필요가 없다.
Drawing Conclusions
중요한 측정 항목이 있는 측정 항목을 파악한 후에는 어떻게 됩니까? 이제 결과가 무엇을 하고 말하지 않는지 결정해야 한다.
어떻게 변화를 결정할 것이냐?
- 나는 통계적으로 의미가 있고
- 변화가 실제로 무엇을 했는지 이해
- 가치가 있는가?
Gotchas 코호트 분석
실험이 올바르게 설정되었는지 다시 확인하십시오. 최종 차이를 보십시오. 실험 측정 항목이 실제로 정상인지 확인 통계적 중요성을 찾는것이 아니라는것을 기억해라 실제로 변경을 시작하면 기회 비용은 얼마인가? 변화로 부터 얻을 수 있는 보상과 관련하여
A/B 테스트
사용자 집단을 나누고? 집단을 어떻게 나누는게 좋을지?
- Session, cookie, User
고객 분석을 위한 테스트
- 종단적 연구 - 코호트 분석
- 횡단적 연구 - A/B 테스트, 다변량 분석
사용자 Funnel
Cart -> Billing and Shipping -> Payment
귀무가설과 대립가설 차이가 나는지 확인
- 귀무가설은 차이가 없을것이다.
-
대립가설은 차이가 있을것이다. (서로 다르다)
- two-sided, one-sided (크다, 작다)
-
유의수준
- 통계적으로 보고 있기 때문에 전반적으로 95%의 경우 (1-0.95) = 0.05가 유의수준이 됨
-
유의확률 (p-value)
- 귀무가설이 맞을 경우에 얻을 수 있는 결과보다 더 극단적인 값이 관측될 확률
- p-value 가 작을 수록 귀무가설과 양립하는 데이터가 나타날 확률이 낮음
- p-value가 작은 경우 귀무가설을 기각함
- p-value의 경우 표본 크기가 커짐에 따라 값이 달라지거나 특정 경우에 값이 커지는 등의 문제가 발생할 수 있음 -> 통계적 유의성과 현실 상에서의 문제를 고려해서 결과를 판단함.
-
비교군의 해당 지표에 대한 신뢰구간을 구한 뒤 실험군의 지표의 크기가 이 신뢰 구간에 들어가는지 (유사), 벗어나는 지를 확인
- t-test 검정
Hypothesis testing in Machine learning using Python
hypotehsis testing 방법론에 대해서 설명
참고
RPM (Revenue per thousand impressions)
- impressioms, quries, pageviews 당 estimated earnings * 1000
- RPM은 광고에서 공통적으로 사용되는 숫자이며, 다른 채널의 수익을 비교하는데 도움이됨.
참고
stats library for Spark
StudentTTest
두개의 샘플간에 동일한 분산을 가정하고, 동일한 샘플 크기를 가정하지 않는다. 동일하지 않은 분산의 경우 Welch’s t-test를 대신 사용해야 한다.
참고
- https://www.gousios.org/courses/bigdata/assignment-spark-stats.html
- https://spark.apache.org/docs/2.3.0/api/java/org/apache/spark/mllib/stat/test/StudentTTest.html
Hypothesis testing in Machine learning using Python
hypothesis testing이 무엇인지, 왜 사용하는지 basic of hypothesis는 무엇인지, hypothesis testing의 중요한 파라미터는 무엇인지?
What is hypothesis testing?
실험데이터를 이용해 통계적 결정을 하기 위해서 사용된다. 가설 검정은 기본적으로 모집단population 모수parameter에 대해 가정한다. 우리가 가정하는 것이 사실이라는 수학적 결론이 필요하다.
Why do we use it?
가설검정은 통계에서 필수적인 절차이다. 가설 검정은 모집단에 대한 두개의 상호 배타적인 진술을 평가하여 표본 데이터가 가장 잘 뒷받침하는 진술을 결정한다. 결과가 통계적으로 유의하다고 가정하면 가설 검정 덕이다.
What are basic of hypothesis?
가설의 기본은 정규화normalization과 표준정규화standard normalization 이다. 우리의 모든 가설은 두용어의 기본에 관한것이다. 표준정규화를 사용할때 z-score와 같은 컨셉을 사용.
- Normal Distribution: normal curve의 모양을 가진 분포를 normal distribution이라고 얘기한다.(=벨모양)
- Standard Normal Distribution: mean 0, standard deviation 1
What are important parameter of hypothesis testing?
- Null Hypothesis: 추론통계inferential statistics에서 귀무가설null hypothesis은 측정된 두 현상 사이에 관계가 없거나 그룹간에 연관성이 없다는 general statement 또는 default position이다. 즉, 기본 가정이나 도메인 또는 문제 지식을 기반으로 한다. 예를 들어 회사의 production이 50 unit/per day 라고 가설 (우리는 이 가설을 기각해야 한다.)
- Alternative Hypothesis : null hypothesis의 대립이되는 가설을 말한다. 보통 실제로 관측되는 결과로 간주된다. 예를 들어 회사의 production이 50 unit/per day가 아니다.
- Level of significance: 귀무 가설을 수용accept하거나 기각reject하는 중요성의 정도degree of significance를 나타낸다. 가설을 수용하거나 거부할 경우 100%의 정확도가 불가능하므로 일반적으로 5%의 유의수준level of significance을 선택한다. 일반적으로 alpha(maths symbol)로 표시되며 일반적으로 0.05 또는 5%. 즉, 각 샘플에서 비슷한 종류의 결과를 얻을 수 있도록 95% 확신해야 한다.
- Type I error: 가설은 사실이지만, 우리가 귀무가설을 기각하면 Type I error는 alpha로 표시된다. 가설검정에서 임계영역critical region을 나타내는 normal curve를 alpha region이라고 한다.
- Type II Error: 가설이 거짓일때, 우리가 귀무가설을 수용할때 Type II error를 beta로 표시한다. 가설 검정에서 acceptance region을 나타내는 normal curve를 beta region이라고 한다.
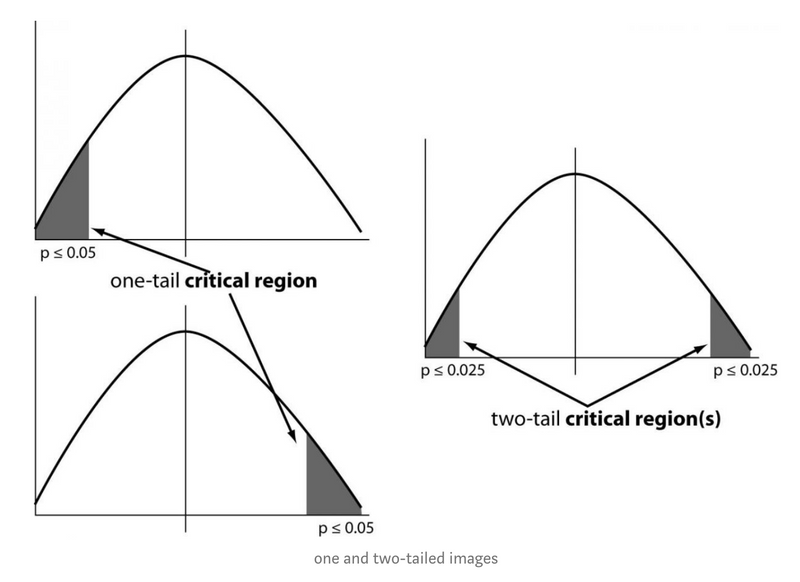
- One tailed test: 샘플링 분포의 한쪽에만있는 통계적 가설 검정을 one-tailed test(단측검정) 이라고 한다.
- Two tailed test: 임계 영역이 양측이고 표본이 특정 값 범위보다 크거나 작은지 여부를 테스트하는 통계 검정. 테스트중인 표본이 임계 영역 중 하나에 속하면 귀무가설 대신 대립가설이 채택된다.
- P-value: p-value 또는 계산된 확률은 귀무가설(H0)이 참일때 관찰된 결과 또는 더 극단적인 결과를 찾을 확률이다. - 극단적인 정의는 가설을 테스트하는 방법에 따라 다르다. P-value가 선택한 유의수준보다 작으면 귀무가설을 기각한다. 즉 표본이 대립가설을 뒷받침할만한 합리적인 증거를 제공한다는 점을 받아들인다. 의미 또는 중요의 차이를 의미하지 안흔다. 결과의 실제 관련성을 고려할때 결정해야 한다.
Hypothesis testing type
- T test (Student T test)
- Z Test
- ANOVA Test
- Chi-Square Test
참고
T-test의 t-value
t-value는 두 그룹간의 차이와 그룹 내 차이 간의 비율이다. t점수가 클수록 그룹간에 차이가 더 크다. t점수가 작을수록 그룹간에 유사성이 더 높다.